GAMES101学习笔记-线性代数基础
2024-12-28
线性代数基础
我整理了GAMES101的图形学课程的学习笔记,我认为这对我很有帮助。
计算机图形学依赖:
| 类别 | 内容 |
|---|---|
| 基础数学 | 线性代数、微积分、统计学 |
| 基础物理 | 光学、力学 |
| 各种 | 信号处理、数值分析 |
| 其他 | 还有一点美学 |
线性代数是基础之一,还是得看。
向量
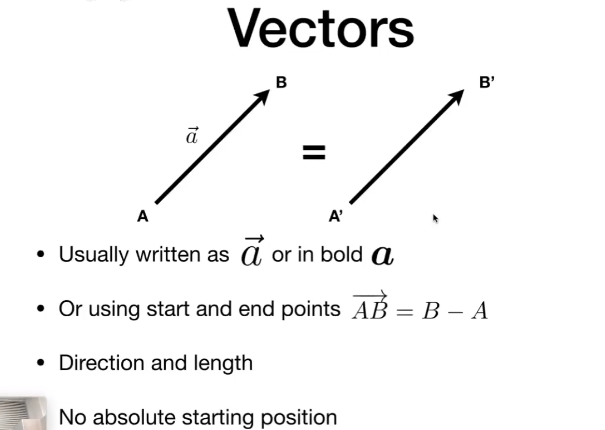
“向量” 是一个 有长度的、有方向的、无原点的方向。
我们默认将向量视为 “列向量”,这在许多领域算是约定俗成的规矩。即:
A=(x, y)^T 或 \ A = \begin{pmatrix} x \\ y \end{pmatrix}
不难看到,向量里并没有和“原点位置”有关的存储信息。
单位向量

向量都有长度。“单位向量” 就是长度为1的向量,适合拿来“仅表示方向,不表示长度”。
把向量除以它的长度,得到的向量就能得到单位向量,使用 \hat{A} (读作A hat)
向量加法
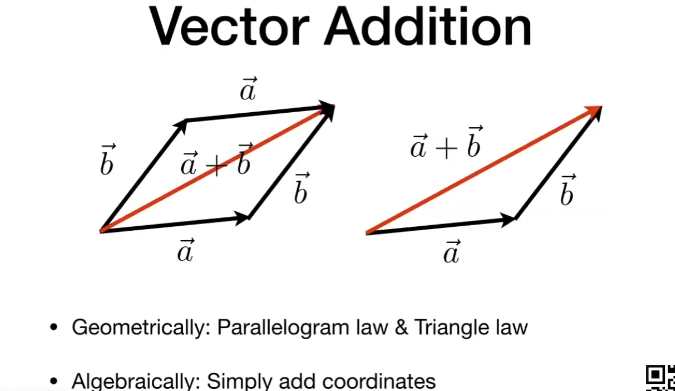
向量间可进行求和操作。所谓求和就是直接相加。显然遵循交换律。
A = \begin{pmatrix}x_1 \\ x_2\end{pmatrix}, \ \ \ B = \begin{pmatrix}x_3 \\ x_4\end{pmatrix}
则,
A+B = \begin{pmatrix}x_1+x_3 \\ x_2+x_4\end{pmatrix}
使用两个“互不相干的单位向量(忘了这种向量的某个特殊专有名词了)”,我们就可以表示二维空间内的任何一个向量了。在笛卡尔坐标系(直角坐标系)中(也就是永远从零点开始,用坐标轴来描述),如果将X、Y坐标轴视为两个单位向量,那么该二维空间内的任何一个向量都可以用这两个单位向量的代数和来表示,即A = uX + vY, X=(1, 0)^T, Y = (0, 1)^T。
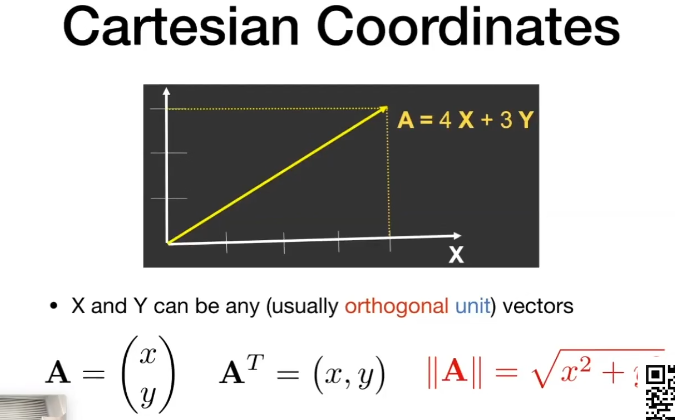
在直角坐标系里,计算长度很方便(勾股定理)。
注意:在图形学里,我们默认将向量视为 “列向量”。
向量点乘
点乘由两个 向量参与运算,所得的结果是一个 标量。
直角坐标系里的计算

在二维直角坐标系里点乘的计算很方便。假设我们有两个向量:A = \begin{pmatrix}x_1 \\ y_1\end{pmatrix}, \ \ \ B = \begin{pmatrix}x_2 \\ y_2\end{pmatrix},则,A与B的点乘结果为 \vec A \cdot \vec B = x_1x_2 + y_1y_2 ,也就是对应元素乘积的和。
在更高维度的直角坐标系里也是同理。例如,在三维空间里,对于向量A = \begin{pmatrix}x_1 \\ y_1 \\ z_1 \end{pmatrix}, \ \ \ B = \begin{pmatrix}x_2 \\ y_2 \\ z_2 \end{pmatrix}, 有
\vec A \cdot \vec B = x_1x_2 + y_1y_2 + z_1z_2
和角度相关的公式
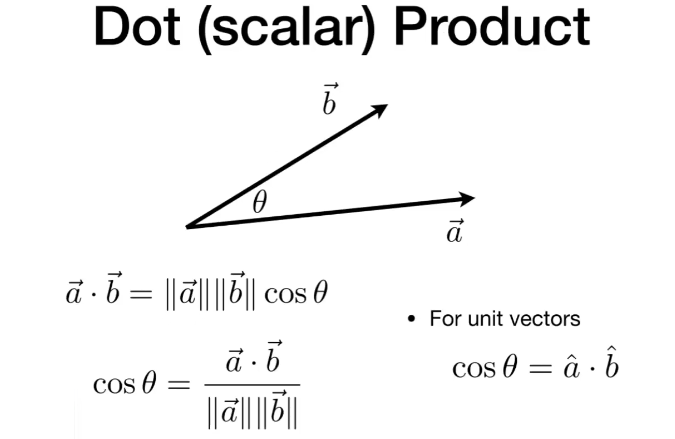
对于向量点乘,有一个很重要的公式,即:
\vec A \cdot \vec B=||\vec A|| *||\vec B||*cos\theta
如果对上述关系式进行简单的变形,则有:
cos\theta=\frac{ \vec a \cdot \vec b }{ ||\vec a|| *||\vec b|| }
给定两个向量,我们就可以算出两个向量的夹角的余弦,从而通过反余弦来得到两个向量之间的夹角。这在计算机图形学中尤为重要。后续计算光照强度、角度,都需要经常用到此性质。
点乘的基本属性
点乘满足以下定义
向量点乘遵循 交换律、结合律、分配率:
\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a} (交换律)
\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c} (结合律)
(k \vec{a}) \cdot \vec{b} = \vec{a} \cdot (k \vec{b} )=k( \vec{a} \cdot \vec{b} ) (分配律)
在图形学里的应用
点乘有许多应用。
快速计算两个向量的夹角

在计算机图形学里,向量点乘可以用来快速得到两个向量之间的夹角。给定任意两个向量,能快速计算出夹角,
即:使用cos\theta=\frac{ \vec a \cdot \vec b }{ ||\vec a|| *||\vec b|| } 快速得到夹角余弦值,再使用反余弦函数即可得到角度。
计算向量的投影、分量
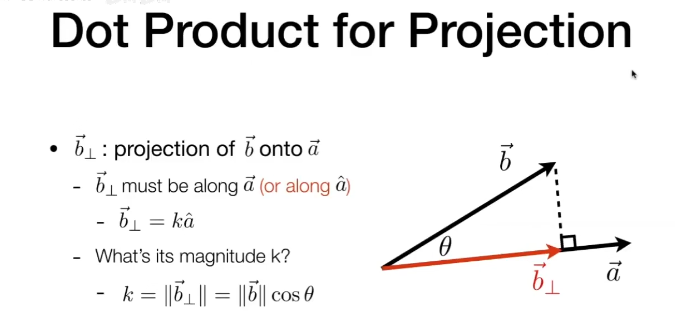
我们还可以利用点乘获取一个向量在另一个向量上的投影、以及在垂直于投影方向上的分量。
例如,我们有A, B 两个向量,它们之间的夹角是 \theta,则:
\vec B_\perp = k \vec A
k = ||\vec b_\perp|| = ||\vec b||cos(\theta)
利用平行四边形法则,我们还能获取\vec B在垂直于\vec A方向上的分量,为\vec B - \vec B_\perp。
有了向量点乘,我们就可以对任意向量进行分解了。
判断向量间的接近程度
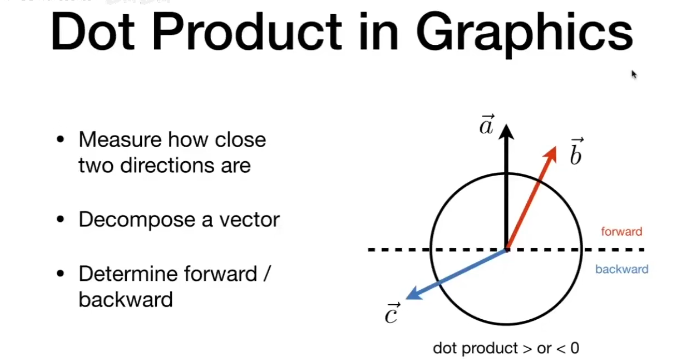
还能根据点乘的积,根据点乘所得结果大小、正负,就能判断两个向量在方向上的“接近程度”。
例如,两个向量的夹角大于90度(是钝角),则它们的方向并不相同,此时它们的点积数值小于0。
当两个向量的夹角小于90度(是锐角)时,它们的点积数值大于0。
如果把这两个向量都视为单位向量的话,不难得知,当两个向量的方向越靠近彼此,它们的点积值就越大(越接近1);反之,当它们越不接近,(也就是夹角越靠近180度)则点积的结果就越小(越接近-1)。
这是很重要的方法。这对于后续 计算光线反射很重要。
向量叉乘
两个向量的叉积会得到另一个新的向量。该新的向量垂直于这两个向量,即,参与叉乘的两个向量所构成的平面。
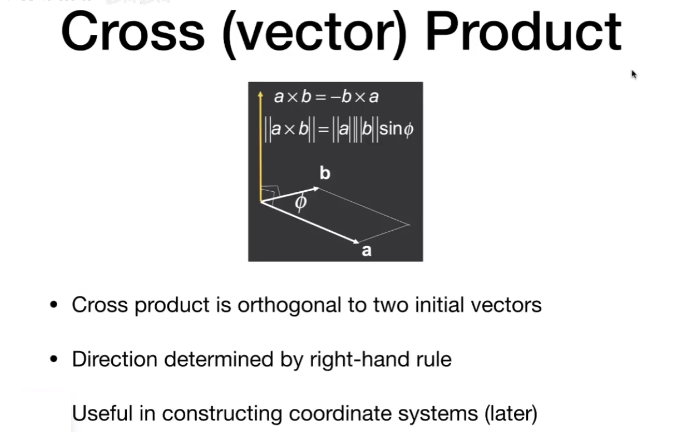
右手螺旋定则:伸出右手握住手,伸出大拇指。如果用四根手指代表“从左边的向量到右边的向量的螺线”,那么大拇指的指向就是新的向量的方向。
叉乘是获取垂直于平面的向量的好办法。
A \times B = -B \times A
||A \times B|| = ||A|| ||B|| sin(\phi) (\phi表示两个向量的夹角)
所得向量的方向可以根据 右手螺旋定则判断方向,也正因此,向量叉积不满足交换律。
叉积可以拿来建立三维坐标系。例如我们可以用两个在x, y平面上的向量,用它们的叉乘来获取z轴向量,从而得到一个三维坐标系。
提一句:如果我们把x,y,z轴分别视为单位向量,那么,如果 x \times y = +z (即,叉积结果为z轴正方向),则该坐标系为右手坐标系(即,符合右手螺旋定则。OpenGL遵循该坐标系);若x \times y = -z则该坐标系为左手系(DirectX常用)。
\vec a \times \vec b = \vec b \times \vec a
\vec a \times \vec a = \vec 0 (长度为0的向量)
\vec a \times (\vec b + \vec c) = \vec a \times \vec b + \vec a \times \vec c
\vec a \times (k \vec b) = k(\vec a \times \vec b)
向量叉积可以直接计算。对于A = \begin{pmatrix}x_1 \\ y_1 \\ z_1 \end{pmatrix}, \ \ \ B = \begin{pmatrix}x_2 \\ y_2 \\ z_2 \end{pmatrix},我们有:
A \times B = \begin{pmatrix} y_1z_2 - y_2z_1 \\ z_1x_2 - x_1z_2 \\ x_1y_2 - y_1x_2 \end{pmatrix}
向量叉乘可以表示为矩阵形式。(暂时没复习到)
向量叉积可以拿来判断“左右”。
例如,我们通过向量叉乘的结果的正负,就能判断一个点在平面上的哪一侧。还可以判断点是否在三角形内部(例如对于P点,判断AB * AP, BC * BP, CA * CP的符号是否一致)。这是光栅化最常用的性质,需要掌握。
在3D空间里,我们可以利用叉乘来定义一些互相垂直的轴,作为坐标系的基。
矩阵
矩阵是一堆数字。 (3 * 2: 3行2列,行:row, 列:column)
例如,\begin{pmatrix} 1 \ 2 \\ 3 \ 4 \\ 5 \ 6 \end{pmatrix}就是一个三行二列的矩阵。
矩阵乘法
两个矩阵能够相乘,必须要确保左边的矩阵的行数=右边的矩阵的列数。
即,两个矩阵的形状是 (M, N) 和 (N, P)。所得的结果形状为(M, P)。
\begin{pmatrix} 1 \ 2 \\ 3 \ 4 \\ 5 \ 6 \end{pmatrix} \begin{pmatrix} 1 \ 2 \ 3 \\ 4 \ 5 \ 6 \end{pmatrix}
在新的矩阵里,每个元素(i, j)都是基于 A中的第i行与B中的第j列的点积。
矩阵乘法不存在交换律!! A B和 B A并不相同!
结合律仍然可用。例如:
(AB)C = A(BC)
A(B+C) = AB + AC
(A+B)C = AC + BC
矩阵和向量也可以相乘。这种情况下,一个n维列向量可以视为 (n*1)的矩阵。
矩阵转置:
即将行与列翻转。使用符号 ^T 来表示。
\begin{pmatrix} 1 \ 2 \ 3 \\ 4 \ 5 \ 6 \end{pmatrix}^T = \begin{pmatrix} 1 \ 4 \\ 2 \ 5 \\ 3 \ 6 \end{pmatrix}
(AB) ^T = B^TA^T
(未完成,有待补充)